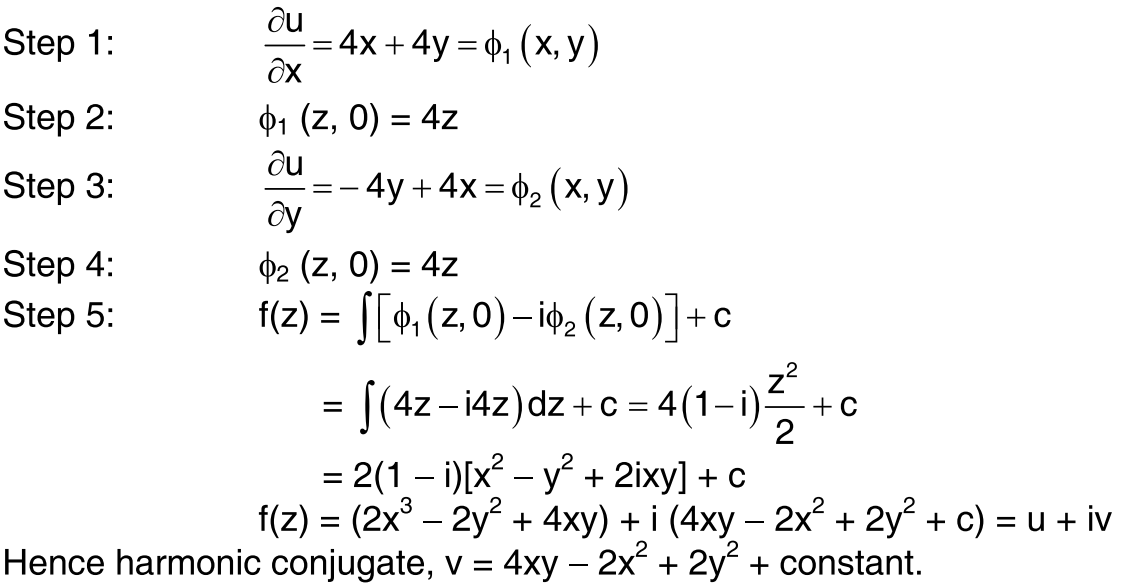Question
A harmonic function is analytic if it satisfies the Laplace equation.
Ifu(x,y) = 2x2 — 2y2 + 4xy is a harmonic function, then its conjugate harmonic function v(x,y) is
Options :
4xy — 2x2 + 2y2 + constant
4y2 — 4xy + constant
2x2 — 2y2 + xy + constant
—4xy + 2y2 — 2x2 + constant
Answer :
4xy — 2x2 + 2y2 + constant
Solution :
Let f(z) = u + iv is an analytic function where u is harmonic then v is called its harmonic conjugate. Here u = 2x2 – 2y2 + 4xy i.e. real part is given, so by using Milne-Thomson method.
Copyright © 2025 Test Academy All Rights Reserved