Question
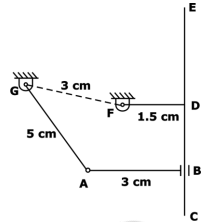
A planar four-bar linkage mechanism with 3 revolute kinematic pairs and 1 prismatic kinematic pair is shown in the figure, where AB ⊥ CE and FD ⊥ CE. The T-shaped link CDEF is constructed such that the slider B can cross the point D, and CE is sufficiently long. For the given lengths as shown, the mechanism is
Options :
a Grashof chain with links AG, AB, and CDEF completely rotatable about the ground link FG
a non-Grashof chain with all oscillating links
a Grashof chain with AB completely rotatable about the ground link FG, and oscillatory links AG and CDEF
on the border of Grashof and non-Grashof chains with uncertain configuration(s)
Answer :
a non-Grashof chain with all oscillating links
Solution :
Here all lengths of links are shown
s = 1.5 cm
l = 5 cm
s + l = 1.5 + 5 = 6.5 cm
Sum of other two links:
p + q = 3 cm + 3 cm = 6 cm
s + l > (p + q)
Grashoff’s law is not satisfied, therefore non Grashoff’s chain.
All are oscillating links or triple rocker mechanism.