Question
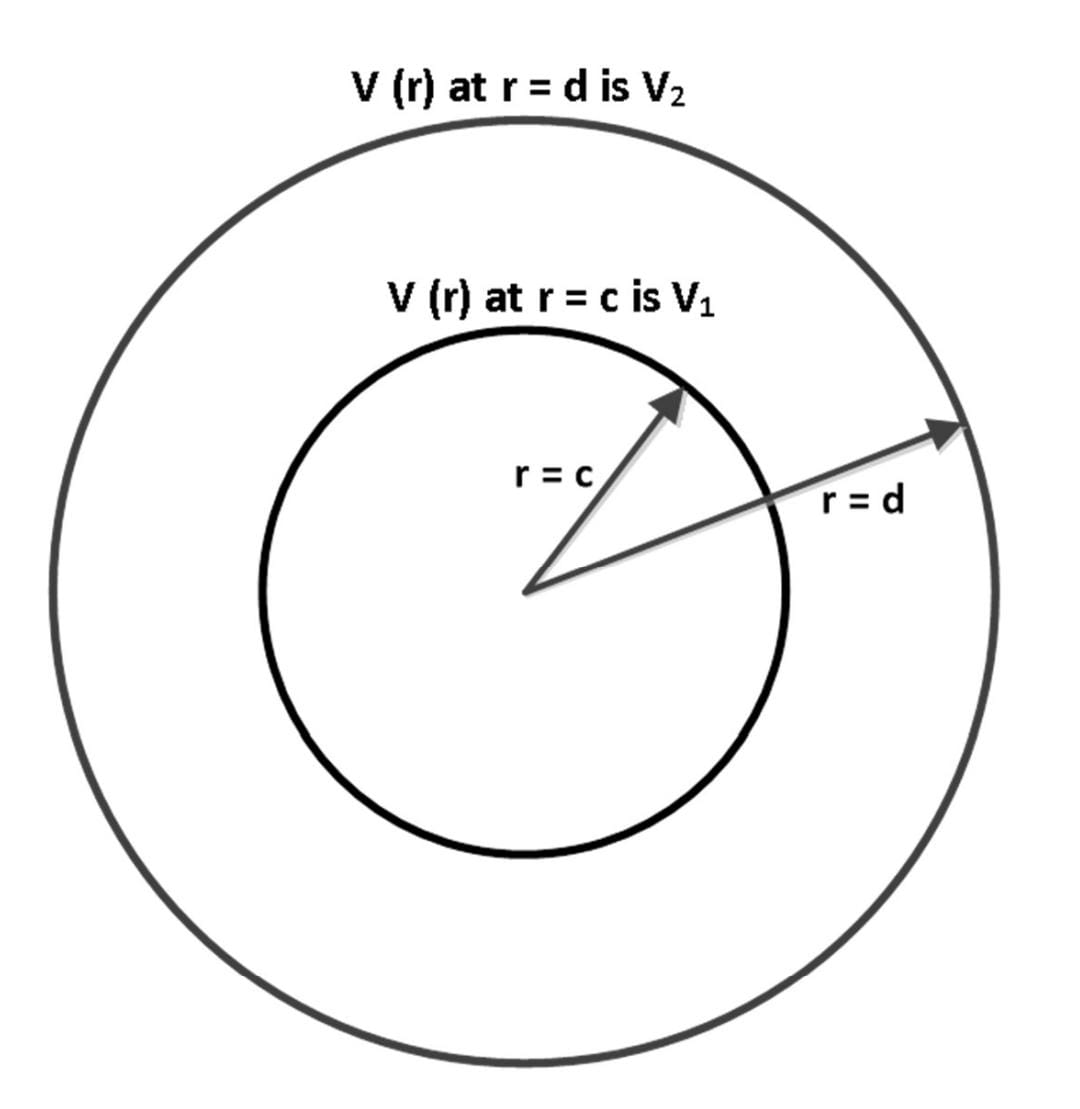
As shown in the figure below, two concentric conducting spherical shells, centered at r=0 nd having radii r =cand r =d are maintained at potentials such that the potential V (r) at r =c is V1 and V (r) at r =d is V2 . Assume that V (r) depends only on r , where r is the radial distance. The expression for V (r) in the region between r =c and r= d is
Options :
V(r)=cd(V2-V1)/(d-c)r - V1c+V2d-2V1d/d-c
V(r)=cd(V1-V2)/(d-c)r - V2d-V1c/d-c
V(r)=cd(V1-V2)/(d-c)r - V1c-V2c/d-c
V(r)=cd(V2-V1)/(d-c)r - V2c-V1c/d-c
Answer :
V(r)=cd(V1-V2)/(d-c)r - V2d-V1c/d-c
Solution :
There is no charge present in side conducting spherical shell (ρv=0), so according to Laplace equation
∇2V(r)=0
Laplacian formula, (only consider r-direction component)
∇2V=1/r2∂/∂r(r2∂V(r)/∂r) + 1/rsinθ ∂/∂θ(sinθ ∂V(r)/∂θ + 1/r2sin2θ(∂2V(r)/∂∅2)
1/r2∂/∂r(r2∂V(r)/∂r)=0
∂/∂r(r2∂V(r)/∂r)=0
Integrate the above equation on both side with respect to r,
r2∂V(r)/∂r = k1 ( ∵ k1 is arbitrary constant)
∂V(r)/∂r = k1/r2
Again integrate above equation on both side with respect to r,
∫∂V(r)= ∫ k1/r2 dr
V(r)= -k1/r +k2 .......(i) ( ∵ k1 is arbitrary constant)
Given at r=c, V(r=c)=V1
V1= -k1/c +k2 ........(ii)
Given at r=d, V(r=d)=V2
-k1/d +k2=V2 .........(iii)
From equation (ii) and (iii),
-k1/d+k1/c = V2-V1
k1=(V2-V1)cd/d-c
Put the value of k1 in equation (ii),
k2=V1+k1/c
k2=V1+ (V2-V1)cd/(d-c)c
k2=-V1c+V2d/d-c
Put the value of k1 and k2 in equation (i),
so, V(r)=cd(V1-V2)/(d-c)r - V2d-V1c/d-c