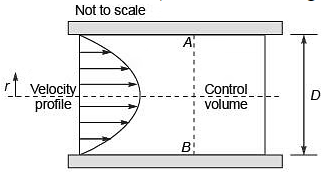
Question
Consider steady, viscous, fully developed flow of a fluid through a circular pipe of internal diameter D. We know that the velocity profile forms a paraboloid about the pipe centre line, given by : m/s, where C is a constant. The rate of kinetic energy (in J/s) at the control surface A-B, as shown in the figure, is proportional to Dn. The value of n is ________.
Show Answer
Answer :
Correct answer is : 8
Now,
∵ (a - b)3 = a3 – b3 – 3ab (a - b)
Report
More Similar Tests