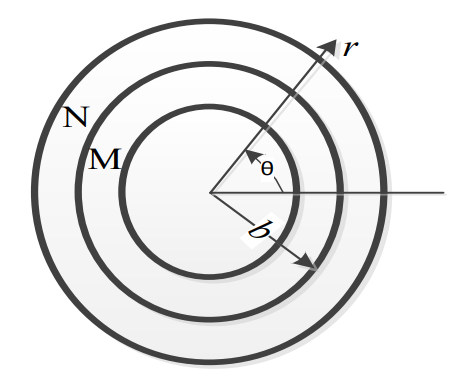
Consider two concentric circular cylinders of different materials M and N in contact with each other at r = b, as shown below. The interface at r = b is frictionless. The composite cylinder system is subjected to internal pressure P. Let (u_r^M ,u_θ^M)  and (σ_rr^M σ_θθ^M) denote the radial and tangential displacement and stress components, respectively, in material M. Similarly, (u_r^N ,u_θ^N)  and (σ_rr^N σ_θθ^N)  denote the radial and tangential displacement and stress components, respectively, in material N. The boundary conditions that need to be satisfied at the frictionless interface between the two cylinders are :