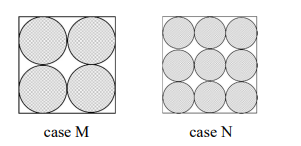
Question
Equal sized circular regions are shaded in a square sheet of paper of 1 cm side length. Two cases, case M and case N, are considered as shown in the figures below. In the case M, four circles are shaded in the square sheet and in the case N, nine circles are shaded in the square sheet as shown. What is the ratio of the areas of unshaded regions of case M to that of case N?
Options :
2:3
1:1
3:2
2:1
Answer :
1:1
Solution :
Both square of case M and N are of radius 1 cm.
Case M :
Let the radius be R
∴ 4R = 1 or R = 1/4 cm.
Area of square = 1 cm2.
Area of circle = 4 × πR2 = π/4 cm2
Area of unshaded region = (1 - π/4) cm2
Case N :
Let the radius be r
∴ 6r = 1 or R = 1/6 cm.
Area of square = 1 cm2.
Area of circle = 9 × πR2 = π/4 cm2
Area of unshaded region = (1 - π/4) cm2
∵ the area of unshaded region in both cases M and N is same, ∴ the ratio is 1 : 1.
Copyright © 2025 Test Academy All Rights Reserved