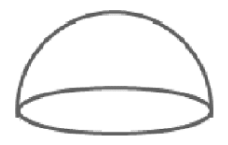
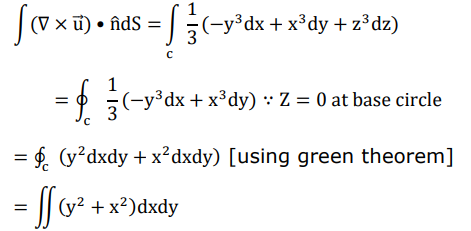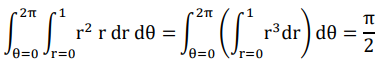Question
Given a vector 
and ˆn as the unit
normal vector to the surface of the hemisphere
(x²
+ y²
+ z²
= 1;z ≥0), the value of integral 
evaluated on the curved surface
of the hemisphere S is
Options :
π
π/3
π/2
-π/2
Answer :
π/2
Solution :
Hemisphere (x2 + y2 + z2 = 1;z ≥0)
To find the integration of the given expiration, it is easy if we are using the stoke’s theorem. Surface integral will become line integral.
Now, putting the value of u in the above
equation.
Now converting the above equation into polar coordinate x² + y² = r ²
Copyright © 2025 Test Academy All Rights Reserved