Question
One-dimensional steady state heat conduction takes place through a solid whose crosssectional area varies linearly in the direction of heat transfer. Assume there is no heat generation in the solid and the thermal conductivity of the material is constant and independent of temperature. The temperature distribution in the solid is
Options :
Quadratic
Logarithmic
Linear
Exponential
Answer :
Logarithmic
Solution :
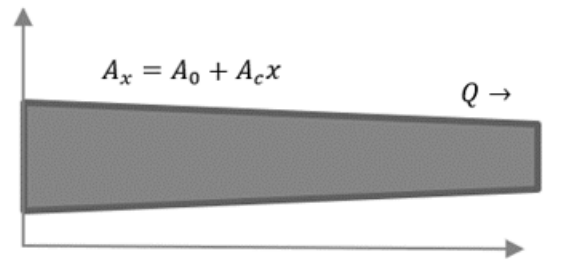
Let the given body cross-sectional area varies linearly, and heat is flowing from left to right.
A = f(x)
Let, A = a + bx
Ein+Eout +Eg = Est (∵ steady state and no heat generation)
Ein = Eout
q ≠ f(x) i.e. is constant
q = -kAcsdT/dx= constant
Acs dT/dx = constant (∵ k will be constant for a material)
∫dT = ∫(C.dx/(a+bx))
T = (C/b)ln(a + bx ) + C1
Hence, temperature distribution in the solid is logarithmic