Question
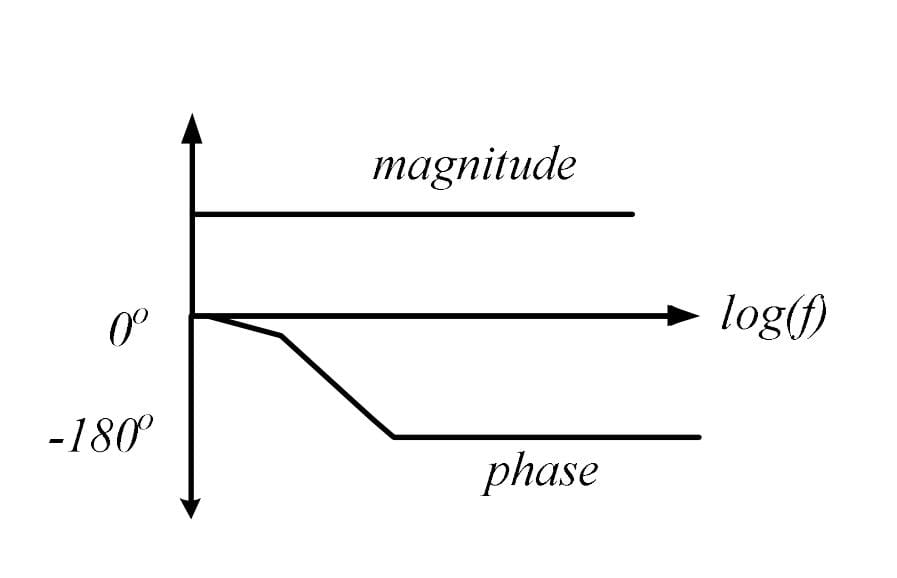
The Bode magnitude plot of a first order stable system is constant with frequency. The asymptotic value of the high frequency phase, for the system, is -180° This system has
Options :
one LHP pole and one RHP zero at the same frequency.
one LHP pole and one LHP zero at the same frequency.
two LHP poles and one RHP zero.
two RHP poles and one LHP zero.
Answer :
one LHP pole and one RHP zero at the same frequency.
Solution :
Flat constant magnitude response for all frequency of system shows that it is an all pass system. In all pass system, poles and zeros are symmetrical about jωaxis. The possible transfer functions all pass system are
T1(s)= s-1/s+1
T2(s)=1-s/1+s
From the phase plot as ω→∞ shows ∅=-180°
For T1(s) :
T1(s)= s-1/s+1
Put s=jω
T1 (jω)=jω-1/jω+1
∠T1 (jω)=180°-tan-1 ω-tan-1 ω=180°-2tan-1 ω
At ω=∞
∠T1 (j∞)=180°-2tan-1 ∞=0°
For T2(s) :
T2(s)=1-s/1+s
Put s=jω
T2 (jω)=1-jω/1+jω
∠T2(jω)=-tan-1 ω-tan-1 ω=-2tan-1 ω
At ω=∞
∠T2 (j∞)=-2tan-1 ∞=180°
Hence, the transfer function of given all pass filter.
T(s)=1-s/1+s
Hence, the system has one LHP pole and one RHP zero at the same frequency.
Hence, the correct option is (A).